三维重建:从基础到3dgs

January 07, 2025

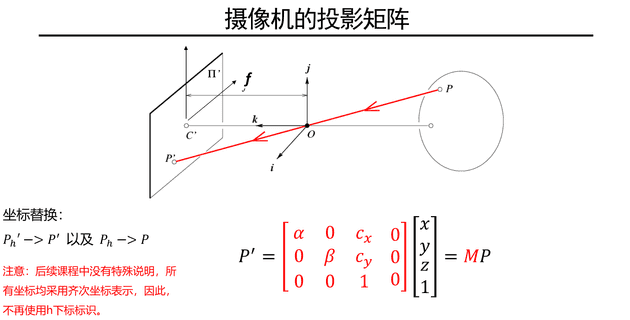
单目相机模型

小孔成像模型

齐次坐标表示: 将三维点用四维向量表示,可以用来表示无穷远点等

如: $P = (x, y, z) \rightarrow P' = (x, y, z, 1)$ ,

其中, $M = K[I 0]$

从影消点到内参矩阵

对于一个直线l,方向为d,无穷远点 $(d, 0)$

无穷远点映射到影消点 $v$ ,因而影消点 $v = Kd$

K为相机内参矩阵

因此可以通过图片中影消点的坐标求出出相机的内参矩阵K

案例: LSS中lift为何能实现距离估计?

基于小孔成像模型, 图像中坐标与三维坐标的关系为:

$\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}$

可以通过先验的 $x$ 和 $y$ 坐标,求出 $z$ 坐标,即实现了距离估计

这种先验信息可以通过深度学习获得,因而LSS中的lift实现了距离估计

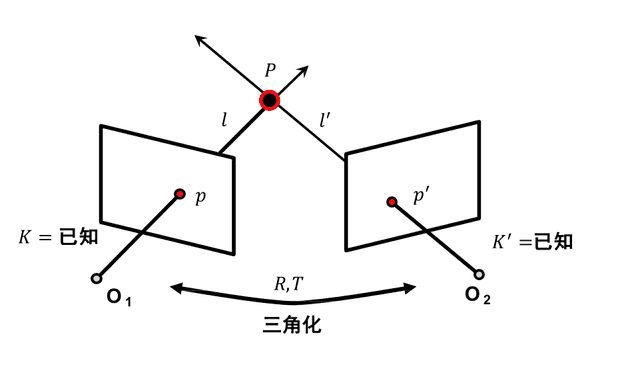
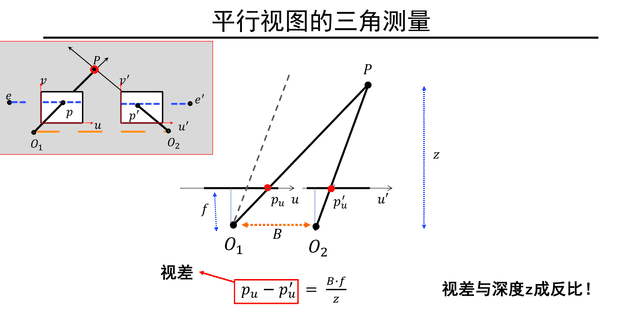
双目三维重建基础

根据图,可以得到公式

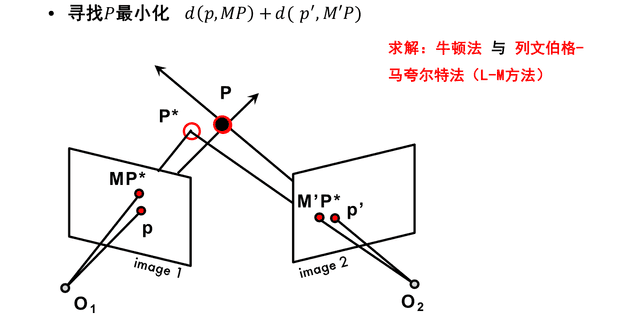
但是由于实际应用中有一定噪声存在,可能两条线不相交,此时应使用非线性解法

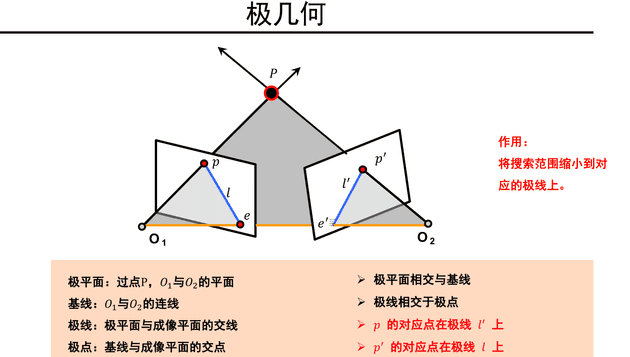
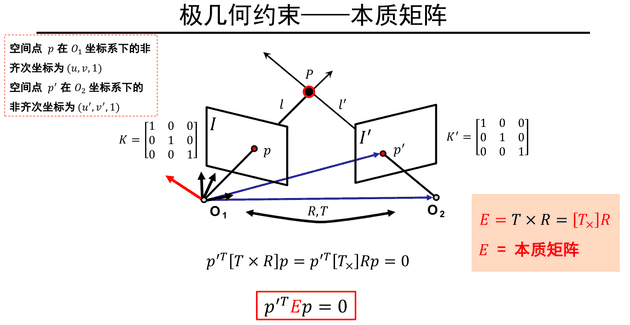
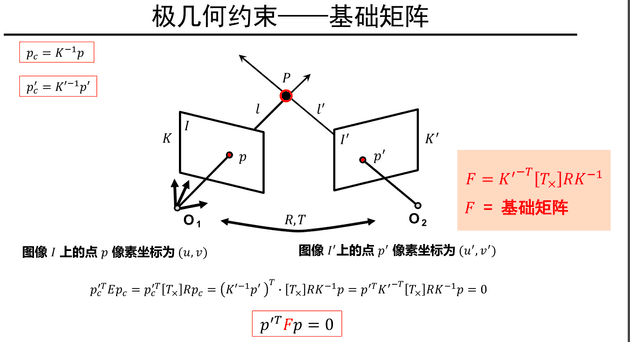
极几何

如何寻找对应点:

基于极几何,可知对应点可以在对应极线上搜索,只需知道 $O_1$ , $O_2$ 和 $p$ 点即可得到 $p'$ 点的线

本质矩阵F自由度为7,如果知道F,无需场景信息以及摄像机内、外参数，即可建立左右图像对应关系（ $p \rightarrow p'$ )

基于三角测量,可以得到三维点 $P$ 的坐标

案例: ok-robot中的三维语义识别重建

遍历所有图片,将对应物体的coordinate记录到semantic memory里面,以便后续导航

代码示意(非完整代码)

    def _setup_owl_dense_labels(
        self, dataset, mask_predictor
    ):
        for idx, data_dict in tqdm.tqdm(
            enumerate(dataloader), total=len(dataset), desc="Calculating OWL features"
        ):
            rgb = einops.rearrange(data_dict["rgb"][..., :3], "b h w c -> b c h w")
            xyz = data_dict["xyz_position"]
            for image, coordinates in zip(rgb, xyz):
                masks, iou_predictions, low_res_masks = mask_predictor.predict_torch(
                    point_coords=None,
                    point_labels=None,
                    boxes=transformed_boxes,
                    multimask_output=False
                )
                #print(masks.shape)
                masks = masks[:, 0, :, :]

                for pred_class, pred_box, pred_score, feature, pred_mask in zip(
                    labels.cpu(),
                    boxes.cpu(),
                    scores.cpu(),
                    features.cpu(),
                    masks.cpu(),
                ):
                    img_h, img_w = target_sizes.unbind(1)
                    real_mask = pred_mask[valid_mask]
                    real_mask_rect = valid_mask & pred_mask
                    # Go over each instance and add it to the DB.
                    total_points = len(reshaped_coordinates[real_mask])
                    resampled_indices = torch.rand(total_points) < self._subsample_prob
                    self._label_xyz.append(
                        reshaped_coordinates[real_mask][resampled_indices]
                    )
                    self._label_rgb.append(
                        reshaped_rgb[real_mask_rect][resampled_indices]
                    )
                    self._label_weight.append(
                        torch.ones(total_points)[resampled_indices] * pred_score
                    )
                    self._image_features.append(
                        einops.repeat(feature, "d -> b d", b=total_points)[
                            resampled_indices
                        ]
                    )
                    label_idx += 1

sfM流程

描述子: 是一种用于描述图像特征的向量,可以用于特征匹配
常用描述子: SIFT, SURF, ORB等

流程:

特征提取: 提取图像中的特征点
特征匹配: 通过描述子匹配,找到两幅图像中的对应点
求解本质矩阵: 通过对应点,求解本质矩阵
三角测量: 通过本质矩阵,求解三维点坐标

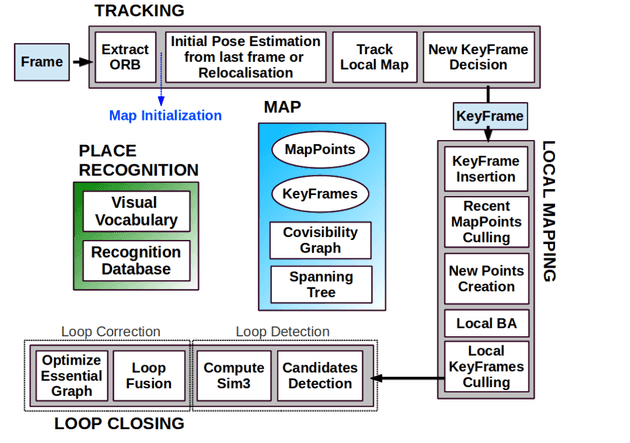
orb-slam

使用orb描述子

闭环检测: 判断是否是同一张图(通过描述子匹配,orb-slam中使用了词袋模型)

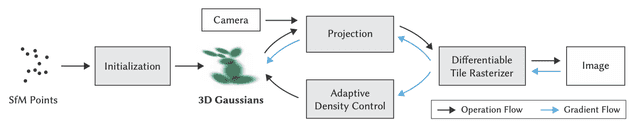
3DGS(3d gaussian splatting)流程

3d gaussian: 三维高斯球
Splatting: 将3d投影到图像平面

通过sfM获得初始3d点
将三维投影到2d image与原image做loss,通过优化得到更好的3d点
点密集化+点剪枝(Adaptive Density Control过程)